- Developable Surface
- Digital Fabrication
- Master
- Milan
- Parametric Design
- Shell Structure
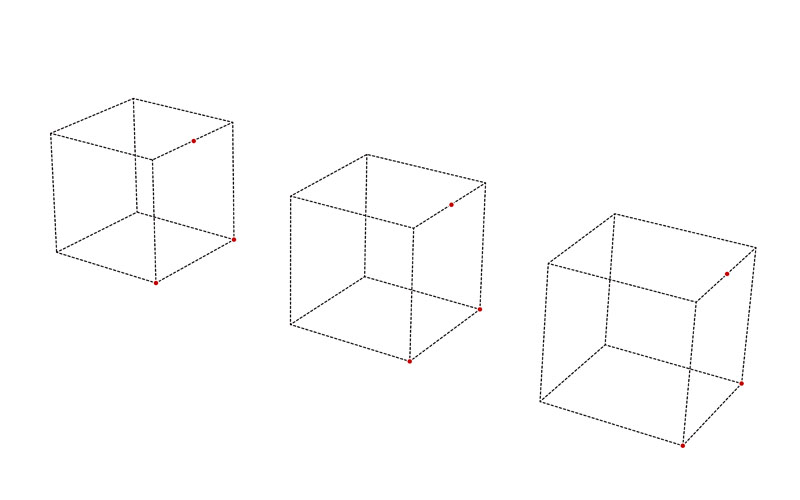
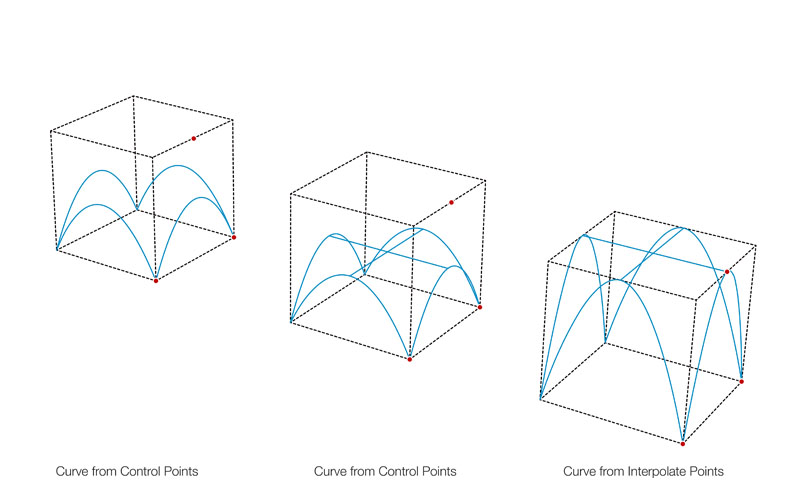
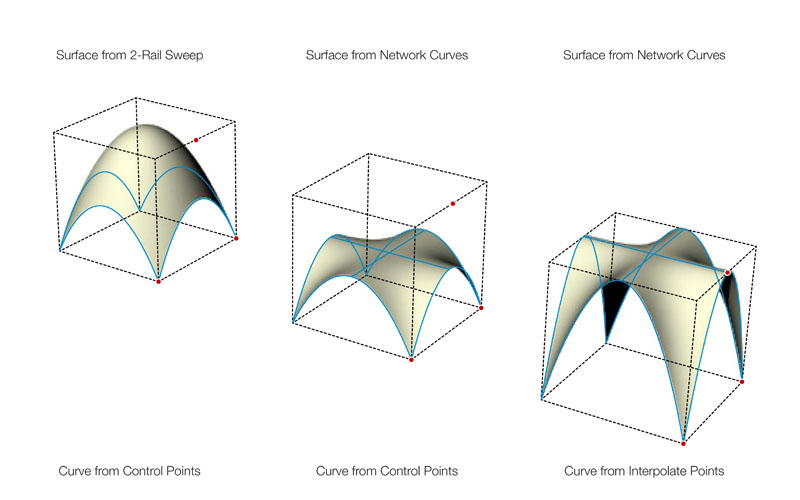
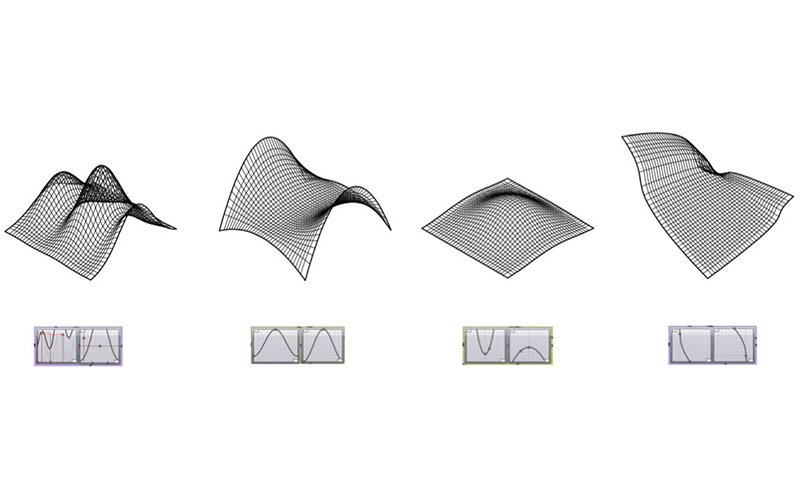
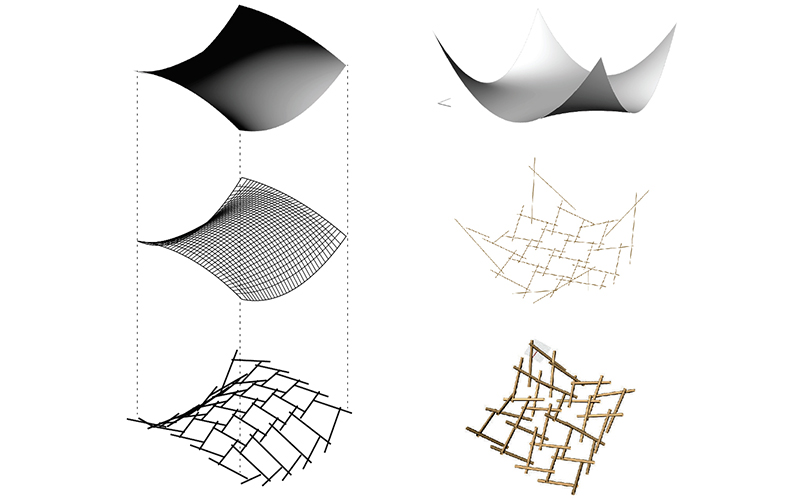
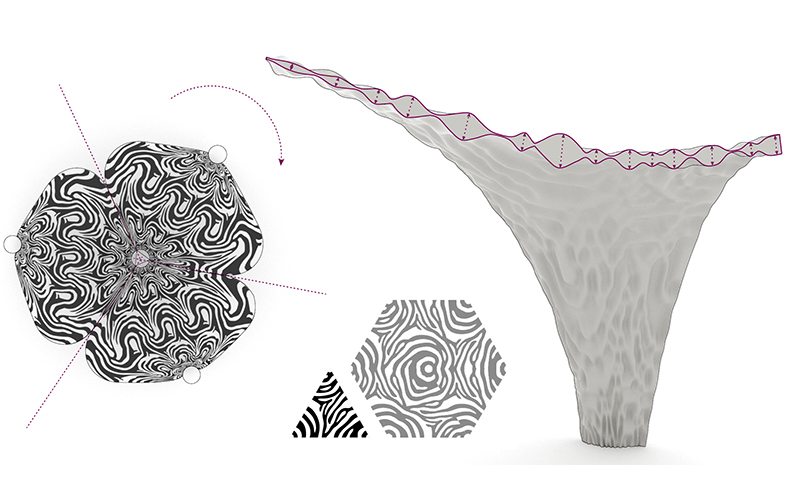
The emphasis of the course was put on research-based design strategies that aimed to unfold hidden complexities of rather simple geometric definitions. 3D-geometries are in first place mathematical objects and as such, they are a sequence of mathematical functions and relations used to describe a set of volumes and surfaces that constitute their separating boundaries. CAD applications are built using these math-ematical concepts but generally, do not unveil them. In order to apply these principles in a comprehensive way, they have to be taught and understood by using the language of Mathematics. Moreover, the constraints that a geometrical shape must satisfy in order to be fabricated conveniently are described as well by mathematical equations.
Taking these aspects into account, the teaching approach combined the definition and discussion of mathematical principles for the generation of spatial geometry and their conceptual, structural, and functional potential from an architectural point of view as well as the potential and constraints for the fabrication of prototypes throughout the process. The considerations exposed above lead to the awareness of the opportunity for Architects to build a familiarity with the basic concepts of Computational Geometry in particular with the representation and approximation of curves, surfaces, and volumes, and showed the necessity to build up a firm knowledge of the language appropriate for the discussion of such concepts.
Credits
Karyna Kalchenko, Karolina Rachwał, Dániel Simoncsics, Gleb Mikhnovets, Alexandre Marguerie, Elizaveta Kunina, Anja Kunic, Aleksandra Rochala, Mateusz Rejniak
Prof. Marco Hemmerling, Prof. Carlo de Falco